Os números sempre desempenharam um papel fundamental no desenvolvimento das civilizações. Desde os primeiros registros de contagem com pedrinhas ou marcas entalhadas em ossos e pedras, o ser humano buscou maneiras de organizar e representar quantidades de forma eficiente. Ao longo do tempo, diferentes povos desenvolveram sistemas de numeração, mas dois deles se tornaram especialmente importantes: o sistema decimal, que utilizamos cotidianamente, e o sistema binário, essencial para a tecnologia moderna. Nesse artigo iremos abordar o sistema binário e sua relação com o sistema decimal.
Sistema decimal
O sistema decimal, também chamado de sistema de base 10, é seguramente o mais antigo e difundido. Além disso, sua origem está ligada ao modo mais natural de contagem que tínhamos disponível: os dez dedos das mãos. Ao passo que civilizações como os hindus, os árabes e os egípcios já o utilizavam em suas práticas comerciais e matemáticas.
Atualmente, o sistema que usamos, conhecido como sistema indo-arábico, foi aperfeiçoado entre os séculos V e IX, principalmente graças às contribuições dos matemáticos da Índia e, posteriormente, à sua difusão pelo mundo por meio dos árabes.
Além de contar com dez algarismos (de 0 a 9), o sistema decimal possui a característica de ser posicional, ou seja, o valor de cada dígito depende da posição que ocupa no número. Assim, no número 472, o algarismo 2 não vale apenas “2”, mas representa duas unidades; o 7 corresponde a sete dezenas, e o 4 indica quatro centenas. Dessa forma, essa estrutura de organização tornou os cálculos muito mais práticos e foi essencial para o avanço do comércio, da ciência e da matemática.
Sistema binário
Em contrapartida sistema binário, de base 2, utiliza apenas dois símbolos: o zero e o um. Embora seja visto como uma invenção moderna, suas raízes históricas remontam ao século XVII, quando o matemático e filósofo alemão Gottfried Wilhelm Leibniz estudou e formalizou esse sistema, inspirado inclusive em antigos textos chineses como o I Ching.
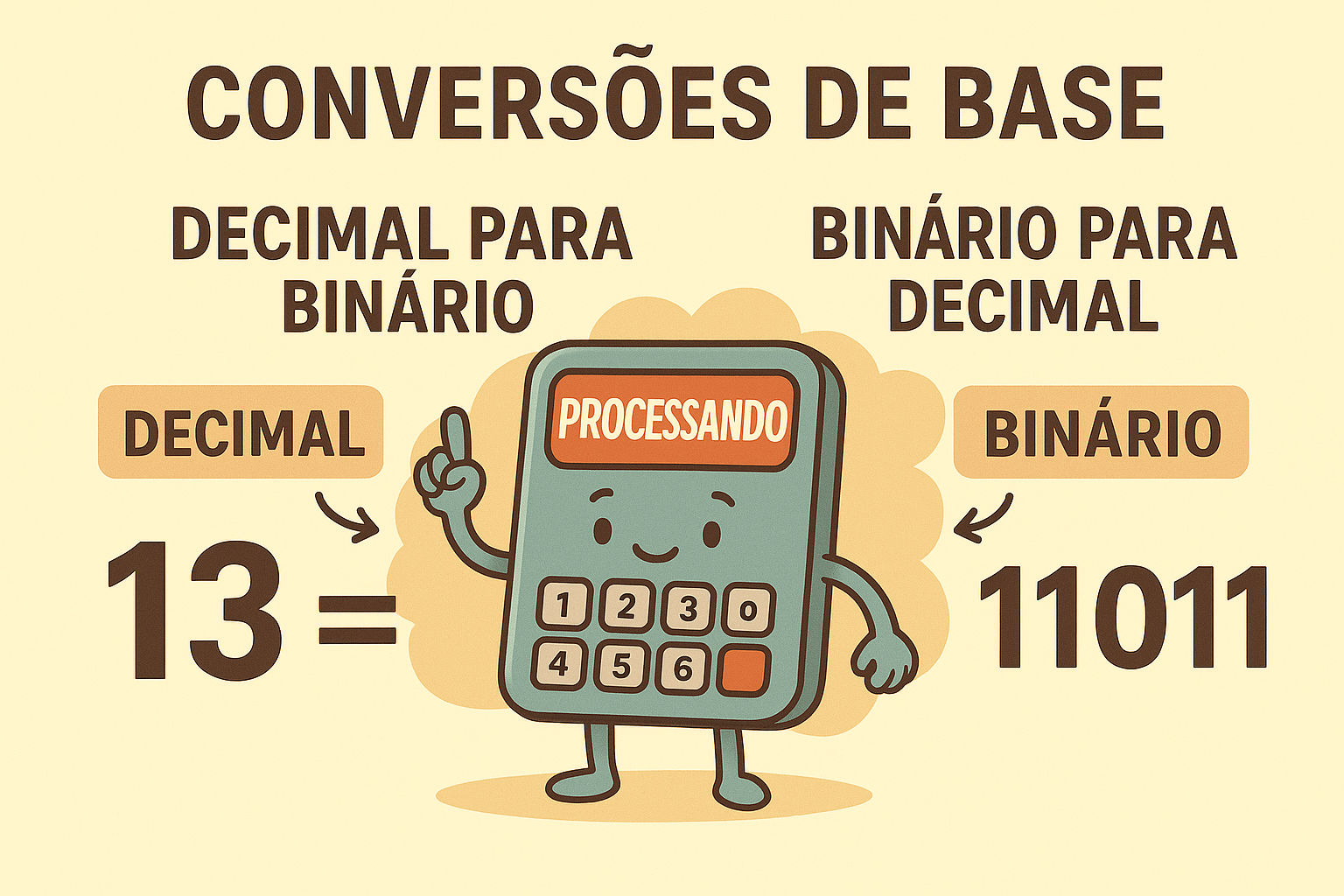
Diferente do decimal, no binário cada posição corresponde a uma potência de 2, e a leitura de uma sequência de zeros e uns resulta em valores inteiros no sistema decimal. Por exemplo, a sequência “1011” corresponde ao número decimal 11, já que seus dígitos equivalem a oito, dois e um somados.
Inicialmente, esse sistema parecia ter pouca utilidade prática. No entanto, com o passar do tempo, ele se tornou a base da computação moderna. Com o surgimento da eletrônica no século XX, ficou evidente que um sistema baseado em apenas dois estados “ligado” e “desligado” em um circuito era ideal para representar e processar informações. Dessa forma, toda a lógica dos computadores, dos smartphones, da internet e de praticamente todos os dispositivos digitais é construída sobre combinações de 0 e 1.
Relação entre as bases decimal e binária
Compreender a relação entre os sistemas decimal e binário é essencial, sobretudo no contexto da computação, onde constantemente ocorre a tradução de números entre essas duas bases. Apesar de parecerem muito diferentes, o processo de conversão de um sistema para o outro é totalmente lógico e segue um raciocínio simples.
Converter decimal para binário
Quando se deseja converter um número decimal para binário, a ideia central é decompor esse número em potências de 2. Isso acontece porque cada posição do binário representa exatamente uma potência dessa base, como 20,21,2220,21,22, e assim por diante. O método mais comum consiste em dividir sucessivamente o número decimal por 2 e observar os restos dessas divisões. Então, cada resto encontrado corresponde a um dígito binário. Por fim, a leitura final é feita do último resto obtido até o primeiro, resultando na sequência que representa o número em base 2.
Vejamos alguns exemplos:
- 14

- 157

- 1789

Converter binário para decimal
O processo inverso, ou seja, converter do sistema binário para o decimal, é igualmente direto. Nesse caso, observa-se cada dígito binário e multiplica-se pelo valor correspondente da potência de 2 associada à sua posição. Em seguida, somam-se todos os resultados, obtendo-se um número equivalente em base 10. Por fim com base nos resultados que encontramos no exemplo anterior, abaixo é apresentado como fazer o processo inverso para chegarmos no valor decimal.
- 11

- 101

- 1001

Ficou com alguma dúvida ? Acompanhe a resolução de problemas de conversão de base no canal YouTube.
Calculadora de conversão de bases
Percebe-se, portanto, que tanto a passagem de decimal para binário quanto o caminho contrário envolvem apenas a interpretação das posições como potências da base em que o número se encontra. No caso do decimal, tratamos de potências de 10 e no binário, de potências de 2. Essa lógica torna os dois sistemas não apenas compatíveis, mas também complementares, permitindo que a matemática humana.
Com a finalidade de aprender, abaixo, encontra-se uma calculadora onde é possível fazer a conversões de base vista nesse artigo.
Conversor Decimal ↔ Binário